Author: Eli McElroy

Posted on

A Time for Reflection

I feel like I have learned how to better use several tools that will help students visualize the mathematics that they are learning.  I practiced using Desmos graphing calculator and thought of multiple ways that I could use it in a lesson.  I also learned about new tools that I have never heard of before, such as GapMinder World.  Overall, I feel like the teaching with data visualization was the most valuable lesson for me.  I could see myself using several of the tools in future math lessons.

The thing that was the most frustrating for me was creating a screencast.  I didn’t like that if I made a mistake while screencasting, I had to go back and re-do the entire video.  I understand that creating screencasts can be valuable – it makes it unnecessary for a teacher to explain the same thing multiple times and allows for time to focus on other tasks during class time. However, I do not think it is a teaching strategy that I will ever use because I found it to be very time-consuming and frustrating to create one short video.

Image credit Moyan Brenn

Posted on

Using Google Forms as a Self-Evaluation Tool

I used Google Forms to create the following self-assessment for students in a pre-calculus class.

Students would complete this form at the end of a semester/quarter.  The intent of this activity is twofold:

  1. In order to receive some feedback about my teaching performance, I ask students to tell me one thing that they thought I did well and one thing they thought I could do better to help them be successful in class.  I can use the student feedback to help myself improve as a teacher.  Initially, I had a field for students to enter their names, but I chose to delete this question so students could answer more candidly.  I also devoted one question to finding out whether or not students think the material they learned will be useful in their lives.  I always try to make math lessons applicable to the real world, and this question tells me how well I did this.
  2. Students are given an opportunity to reflect on their own performance throughout the semester.  They might consider if they need to stay more organized, put forth more effort, or ask more questions.  The intent is that students reflect on their performance and then improve in following semesters.
Posted on

Visualizing Mathematical Functions

One data visualization tool that would be helpful for students to use in a math classroom is Desmos graphing calculator.  I could use Desmos in a lesson about graphing sinusoidal functions.  I might begin the lesson by instructing my students to log on to Desmos and simply modify the equation y=sinx in any way that they wish.  I would instruct them write down what they observe as they do so.  After they have had some time to explore, I might provide a worksheet for some more guided practice.  The worksheet might ask them to do things such as add a constant to the equation y=sinx and observe what happens.  Students should notice that the graph is moved up by whatever constant they added, like in the image below.

The worksheet might also ask them to multiply the sine curve by a constant.  When doing so, students should notice that the sine curve gets taller.

The use of Desmos graphing calculator allows students to quickly and easily see how modifying the equation y=sinx changes the graph.  Once students have any idea of different modifications change the graph, I would introduce formal vocabulary for the modifications.  For example, adding a constant creates a vertical shift and multiplying by a constant changes the amplitude of the sine curve.

Image credit: Dylan Ng

Posted on

What’s Your Sine?

1. Learning Objective

Students will be able to find the derivatives of sinusoidal functions.

2.  Digital Resource(s)

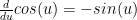Before coming to class, students will watch an online video that I will create of me proving \frac{d}{du}sin(u) = cos(u) and \frac{d}{du}cos(u) = -sin(u).

3. Active Learning Strategies

Once students have an idea where the equations come from, they can use the freed up class time to solve problems where they are asked to find the derivatives of sinusoidal functions.  One active learning strategy that I might employ is Numbered Heads Together.  I will split students into groups of three or four and have them collaboratively work on problems that I will provide.  One randomly selected student from each group will then provide a brief explanation of how their group went about solving the problem.  Students who would have difficulties solving the problems on their own will have the benefit of group members to help them out.

4. Lesson Flow

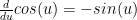The video explains to students where the equations \frac{d}{du}sin(u) = cos(u) and \frac{d}{du}cos(u) = -sin(u) come from.  I will begin class by demonstrating to students how we can use these equations to find the derivatives of various sinusoidal functions.  The example problems will require the use of techniques taught in previous lessons such as the power rule, the product rule, and the chain rule.  After the example problems, students will be split into groups for the Numbered Heads Together activity where they will solve some problems in groups.  Finally, students will be given some homework problems to work on individually for the last part of class.

5. Benefit for Students

As a math teacher, I dislike presenting a formula or equation to students and asking that they believe it on blind faith.  I really believe that students benefit from seeing where formulas come from and why they work the way they do.  However, in many classes (especially calculus), there are simply too many equations to offer a formal proof for each one during class time.  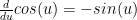By flipping this lesson, students are able to see where the equations \frac{d}{du}sin(u) = cos(u) and \frac{d}{du}cos(u) = -sin(u) come from, and I won’t have to use class time to prove the equations.  Instead, students can use class time to collaboratively work on problems where they will apply the equations.  This is preferred to having students work on problems at home, where they would not have a teacher or classmates to help them out if they get stuck.

Image credit: Creativity103

Posted on

Inequalities with Desmos Graphing Calculator

I used CaptureSpace to record an instructional video on how to graph inequalities with Desmos graphing calculator.  I thought using CaptureSpace was a fairly straightforward process, which isn’t how I normally feel after using a program for the first time.  I was easily able to record my video and upload it to the UP media page.  In the future, I could see myself using a screencast to explain to students how to use technology, such as the Desmos graphing calculator or even certain functions on a Texas Instruments calculator.  I could also use it show mathematical proofs for things that I don’t have time to prove in class.  For example, if I want my students to know that the derivative of sin(u) is cos(u), but I don’t have time to show a formal proof in class, I could give them access to a screencast of me proving it.

One thing I don’t like about screencasting is how difficult it can be to fix mistakes.  For example, when I re-watched the embedded video, I realized that I made a mistake at the 1:33 mark – I said the circle had radius 4 when I meant to say that it had radius 2.  This was a small mistake, so I just let it slide for the purposes of this assignment.  However, if I was sharing a video with my students, I would not want them to be confused by a mistake on my part.  Therefore, I would probably have to go back and re-shoot the entire video just to fix one mistake.  And then if I noticed I made a mistake in the re-shoot, I might have to record yet again!

Featured Image: Sykez Tom

Posted on

Digitally Exploring Oregon’s Native Plants

For this task, I chose to collect public domain sources related to the native trees and plants of Oregon.  After fiddling around on Microsoft OneNote for a few minutes, I felt as though I was completely incapable of operating a computer.  There were so many toolbars and sidebars that I had no idea where to go or what to do in order save my sources.  I decided to switch over to Google Keep instead.  I found Keep to be fairly easy to use.  The user interface of Keep was a lot simpler and didn’t have nearly as many options as OneNote, which I personally find to be a good thing.  I downloaded Keep as an extension to my Google Chrome browser.  Every time I found a source that I was interested in saving, I simply clicked on the Keep logo in my browser’s toolbar and a link to the webpage was saved in Keep.

I found a few of the public domain search tools to be very helpful.  Flickr was a great source for finding images.  It was easy to search for images and identify the type of license associated with each image.  My only problem with Flickr was that many of the images were incorrectly labelled by the person who posted them.  For example, I found this image of a lady fern when I was searching for a sword fern.

I’m not a plant expert, but I was able to identify several other images on both Flickr and Google Images Creative Commons Search that were incorrectly labelled.  This could potentially be a problem for students who are researching native plants for a school project.  Incorrectly labelled images might cause confusion about what plants look like.  On the other hand, it might be good practice for students to filter through information and identify which sources are reliable.

 

Image credit to vladeb

Posted on

Limited Technology at Barlow

During my fall placement, I did not make much use of technology in the classroom.  The most frequently used technology tools in my classroom were a document camera and projector.  I taught almost all of my math lessons by writing notes on paper under the document camera and projecting it onto the whiteboard.  I felt like using the document camera was an effective use of technology for several reasons.  First of all, my classroom had the document camera positioned in such a way that I could be facing my students while going over lessons.  This allowed me to make eye contact and project my voice toward students, which is a nice alternative to turning my back to them while writing on the whiteboard.  Using the document camera instead of writing on the whiteboard also allowed me to save the notes I went over in each class so that I could easily give a copy of the notes to students who were absent.  Finally, students were easily able to share and explain their work to the class by putting it under the document camera and projecting it on the whiteboard.  Aside from the document camera and projector, there was very little technology used in my placement.

Part of the reason why I rarely used technology in the classroom was the lack of technology available to the students in my placement.  There were no Chromebooks or laptops available for my students to use in the classroom.  If I did want students to have computer access during class time, I would have needed to reserve a computer lab and wait for my students to logon to outdated, mismatched desktops.  I feel like this is not an effective teaching strategy when class periods are only 50 minutes long, as too much of the period would be spent just getting students onto their computers.

In this class, I am hoping to learn more ways that I can implement technology into my math classroom.  Technology can allow students to participate in guided exploration to discover mathematics on their own.  It can also provide a way to share visual-learning tools with students to improve understanding.  In addition to using technology in the classroom, I also hope to learn some ideas for how I can assign supplementary tasks for students to complete outside of the classroom that can make use of the technology that they have in their homes.

 

Image credit to Adam Freidin https://www.flickr.com/photos/-adam/4674856117/in/photolist-886RRx-54G3F9-7MFi3u-5Y8et-aWrnk-9eBxh-4jhjQ-9aKxBs-92nj2T-2XNVQ-Gea4J-4RJSUp-9WNA8B-9kY44t-bc1djK-66GAT5-djjTPy-7qcqsn-mehzo-do77gr-5PmwPt-djkci6-mehsi-5UTQB5-7YRqV8-4nLgbx-9Cv3HE-aYnHpF-5Y8aT-5Y8co-4kzEVP-zGRAz-fRYLeC-4BgAPn-bUf8df-5ndsQu-qwtr1j-4BYSwC-2pUEss-8qvWnw-ckGzJG-9xBJ67-ewpdD-rj9p3Y-jDZPJF-a9Rq2n-bxWuxa-ewxdfS-6Y1Rbx-ewu3v8